
Where am I Vertically? Why is that my altitude?
Mount Everest is commonly known as the highest mountain on earth with an elevation of 8,848m above sea level (Wikipedia, 2015). But what does that mean?
It is the height above mean sea level, which was calculated by a group of surveyors who measured from the shore line to the base of the mountain and all around the country where they laid benchmarks showing the height above or below their starting point at the coast line. From these benchmarks the surveyors could use mathematics called triangulation to calculate the vertical distance from the benchmark to the top of the mountain.
So is this really the highest mountain on earth? Compare it with some other mountains in the table below:
The Australian Height Datum (AHD) is the official height datum for Australia. Elevation/altitude is measured from AHD to the object or peak. From 1945 -1960 surveyors completed level runs from 30 different tide gauges around the country inland where they installed bench marks that identify the height at each mark in relation to the tide gauge they started from see the figure below. This datum is called AHD71. In Tasmania another level survey was completed creating AHD83 or AHD-TAS83 (ICSM, 2013). Commonly the term AHD is used for the whole country.
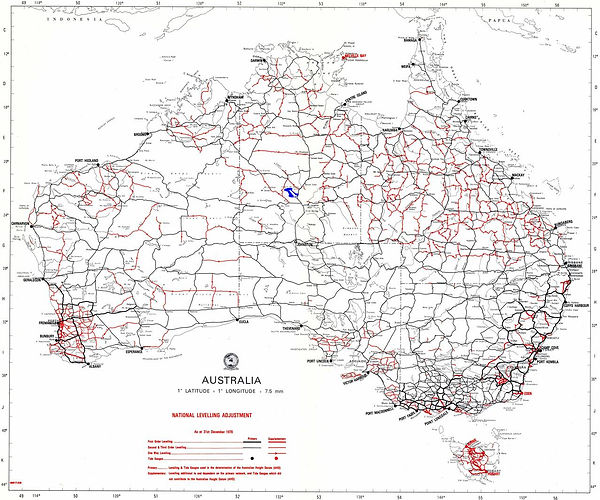

Map of the Level Runs Creating AHD
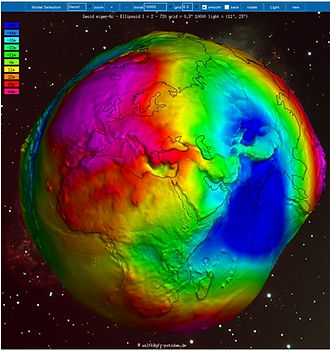
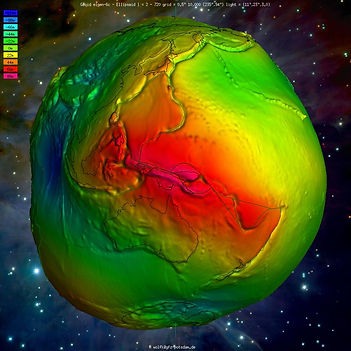
The images above (IAG, 2015) show the difference between the ellipsoid and geoid surface as a function of gravity. This shape represents something close to the actual mean sea level around earth. The colours represent the undulations above and below the ellipsoid. The undulations (colour scale) ranges from -110m-88m. GPS/GNSS measurments on the default WGS84 datum, measures heights from a point on earth to the ellipsoid. We want to know our elevation/altitude above sea level which is the shape above. Therefore, there is a chance that the altitude shown on the GPS reciever could be between -110-88m wrong.
Earth as a shape of Gravity

Which surface are you meauring to?
There are 2 surfaces & a datum to be considered in determining elevation:
-
Ellipsoid - smooth surface);
-
AHD- physical measure from beach to land (datum);
-
AusGeoid09 – surface. An irregular shape, based on gravity and land observations.
Use Separation Values to moved between surfaces.
The green line represents land. If you stand on the land (green line) with a GNSS reciever you are finding out the distance from the ellipsoid (blue) to where you are standing - the Elipsoidal Height...unless you have the reciever set up otherwise.
If you then apply an 'N' Value to that elevation you are measuring your height above AusGeoid09 (red)-close enought to be AHD. In some places this will provide high accuracy, in others not so good.
If you measure your elevation using a total statation & a permanent survey mark on the ground, you are finding the height from AHD (yellow) to where you are standing - AHD71 Height.
AHD & AusGeoid09 are close but not exactly the same. Consider three important factors:
1. Gravitational force is affected by land mass.
2. We use the measure of gravitational force to determine what mean sea level would be over land.
3. Mean sea level is different around the world due to effects such as salinity and temperature.
Now consider the two measures of elevation determination in Australia – AHD & AusGeoid09.
AHD is a physical measurement on land. The result of lots of long level runs (measure the difference in height between a point behind and a point in front). Therefore it does not take into account the change in gravitational force across land.
AUSgeoid09 is a model created from gravity measurements and GNSS surveys. As the sea in northern Australia is much warmer and less dense than the cooler waters in the south, mean sea level is different by about 1m from north to south.
In relation to AUSgeoid09, mean sea level (AHD) is approx. 0.5m above the geoid in the north and 0.5m below in the south.
A note on using older geoid models for Australia:
“Older versions of AUSgeoid ('93, '98) are predominantly based on satellite and terrestrial gravity observations which were a best fit of the Geoid over Australia (Brown, 2010). These AUSgeoid versions, referred to as gravimetric geoids, do not account for the one metre offset trend between The Geoid and the AHD. As a result, when using these versions GPS users can only retrieve AHD heights to within ±0.5 metres” (Brown et al., 2010).
Brown, N. (2010) AUSGeoid09: Converting GPS heights to AHD heights Retrieved from http://www.ga.gov.au/ausgeonews/ausgeonews201003/ausgeoid.jsp
 |  |
|---|---|
 |  |
 |
AusGeoid09 Modeled against the ellipsoid

AusGeoid09 Modeled against the ellipsoid
Satellites communicate information to receivers on earth, which is run through mathematic equations to produce the position & elevation information shown on a GNSS receiver. The maths behind the process requires a geometric regular surface to use as a reference. As mean sea level is not a regular shape and neither is the terrain of earth, the ellipsoid shape is used as a best approximation and then corrections are made to obtain an accurate value.
This correction is called the Separation Value or the ‘N’ value and is shown in the figure below. Separation Values are different in different locations. Elevations determined by GNSS receivers alone, calculates the elevation from a point on earth to the ellipsoid shape. In Australia, his can be up to 70m different to the actual value above mean sea level.
The point in the middle is Connor Well where four traverses met. The difference of height between the traverses was up to 1.4meters. (Wise, 2014)
Internationally we consider mean sea level to be the point from which we start measuring height but this is more complicated that just taking the average of tides. Sea levels are affected by gravity which pulls water around. But gravity is not constant around the earth due to differences in the density of the large ununiformed mass full of moving liquid which is earth.
Sea level is also affected by water salinity and temperature. This results in mean sea level being at different levels around the world. In Australia, mean sea level changes approximately 1m from South to North as the water temperature increases in the far north (Brown, 2010, Geoscience Australia).
A visual representation of gravity around earth is shown in the figures below. These are shots from an interactive online service provided by IAG as part of the International Centre for Global Earth Models.
