
Where am I on earth? Horizontal positions
This is an unsual way to describe horizonal positions,
for all the usual explainations see the links page.
Recipe for a position on earth:
The common description for a location on earth is latitude and longitude.
In the past this was the result of calculations from the stars and time,
But over the decades we have changed our methods of calculating the latitude
and longitude of a place and with each new method has come increased
accuracy and usability.
So in today’s world what is the recipe for the description of a location?
Recipe for Location in Australia in 2015
Ingredients:
A lot of Pieces of measuring equipment at certain locations around Australia & the world
A lot of GNSS satellites
A lot of Data about gravity, land mass, tectonic movement, and
our position relative to other land masses and items in space.
1x International Terrestrial Reference Frame (ITRF) 1992 Vintage
1x Ellipsoid, use GRS80 style
1x Australian Fiducial Network (AFN)
1X Australian National Network (ANN)
1x Centre of earths mass
1x Geocentric Datum of Australia with location data at date 1994 (GDA94)
1x Map Grid of Australia designed to fit GDA94 (MGA94)
Method.
In short –
Extract data from a lot of measuring equipment around the world using an International Terrestrial Reference System (ITRS) and GNSS satellites. Mix with extra data and form an ITRF. Combine ITRF with AFN and ANN to create a GDA datum. Place in a GRS80 ellipsoid bowl and place over the centre of earth to get a slightly squashed ball of latitude & longitude lines. Set to locational knowledge of 1 January 1994 and call the resulting coordinates GDA94. Squeeze out positions using a UTM method to produce coordinates on a flat piece of paper and place in a calculator to scale out distortions and rename coordinates as Easting and Northing in MGA94 format. Goes well as a compliment to WGS84 but never a perfect match. Best consumed before the next datum is release in 2020.
The longer explanation:
Step 1:
Choose a lot of places around the earth to place special measurement instruments and constantly monitor their positions using GNSS (Global Reference System).
Use the data collected about the past and present position of these places to create a framework to measure from (Global Reference Frame such as ITRF).
Step 2:
Consider that the earth is constantly moving and that it has a complex irregular shape. It is essentially a massive piece of rock full of moving liquid, covered in mountains and holes. This is not so easy to measure so we need to find a way to make the maths behind the measurements a bit easier.
Imagine trying to pin point the coordinates of a point on a ball of jelly which is being wobbled. Our coordinate system is like a wire mesh around it. The jelly wobbles underneath.
To do this:
Take one ball (sphere) about the size of Earth and position it over earth, as best you can using the Global Reference Frame.
Draw lines around the shape which all meet at the poles (longitude) and lines around the middle (latitude). The calculation of these lines is dependent on angles from the centre of the sphere.
Squash the ball a bit top to bottom (flattening) creating an ellipsoid (such as GRS80). Do this because the actual shape of the rock we call earth is wider around the equator than it is around the poles.
Step 3:
Scale the ellipsoid down and rotate it to fit the land mass you’re in. Choose a point to centre the ellipsoid over. Now with ellipsoid design and position we have created a datum (such as GDA94 or WGS84). These days the trend is to centre the ellipsoid over the centre of earths mass.
Now you have your land mass inside an ellipse (ellipsoid GRS80) of a known size, shape, rotation and you know where the centre of it is in relation to the land (datum GDA94). We also know that this mesh is in relation to the rest of the world because it was created using the global reference frame (ITRF).
So now we have created a way of measuring positions on our piece of land which is mathematically possible and the best estimate we have with the technology and knowledge available to us. Coordinates such as latitude and longitude sit on the mesh and do not move.
This sounds like a great solution, but we still have two real world problems to address:
1. How do we draw this curved surface on a flat piece of paper?
2. If the mesh holding the coordinates is fixed, what happens when the land moves with continental drift and earthquakes?
Solutions:
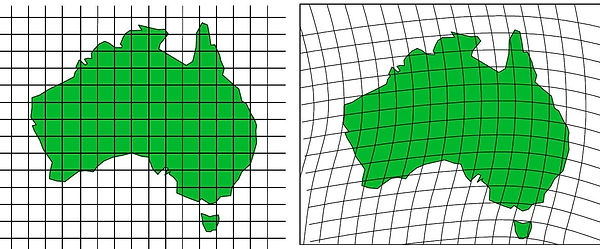
1. Use a set of mathematical equations called projection to put the coordinates onto a flat sheet. Projections are not a perfect system and distortions are always present. Click the red button to see the map experiment.
So we choose a projection appropriate for our area which doesn’t distort our area of interest. In Australia it was decided to use a projection called Transverse Mercator which can be thought of as covering our land in ink, and rolling it over paper in 60 different sections. Click the orange button to find out more about this type of projection.


These diagrams show UTM projection. It is made up of 60 sections of earth where you can imaging paper was wrapped around earth & then tightened so that the earth cuts though it.
This is why we have different scale factors where the paper cuts the earth and where it is above/below.
It takes a little imagination but it produces one of the least distorted maps!
We use the scale factors when changing from latitude/longitude on the ellipsoid to easting northing on the flat sheet.
This image was sourced from Pennsylvania State University (2014)
https://www.e-education.psu.edu/geog862/node/1817.
The origional source was GPS for Land Surveyors.
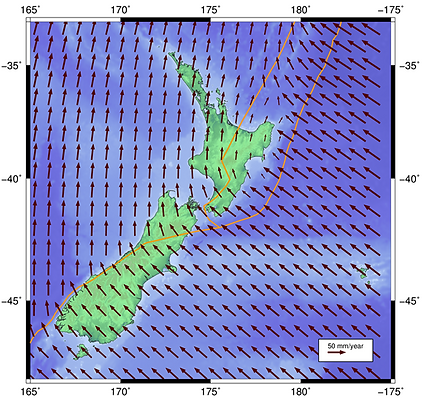
"Average plate tectonic movement relative to ITRF96" (LINZ, n.d) Source: http://www.linz.govt.nz/data/geodetic-system/datums-projections-and-heights/geodetic-datums/new-zealand-geodetic-datum-200-0
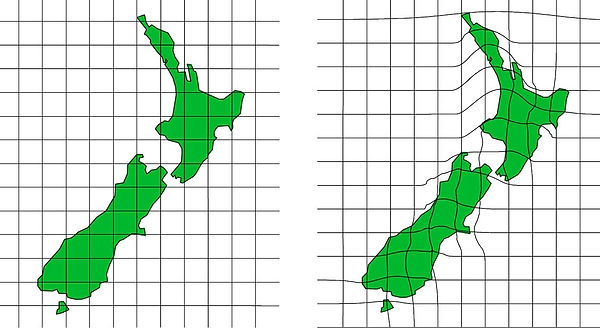
If we fixed coordinates to the land it would be a mess! Due to tectonic movement
Our neat tidy Grid Reference System
Warping Grids
If we kept coordinates stuck to points on the earth, our reference system would skew possilby like the figures below:
So the fundamental question is for people who set coordinates for earth is: How can we set coordinates over the world which are accurate, allow for land movement, and fit the random shape of the earth?
Scientists and mathematicians around the world have been working on this problem for centuries which is why we have multiple solutions. Different knowledge, tools and environment equates to different solutions. There are different solutions to the measurement problem for every country and within each country there have been different solutions developed over time. (Australia has been known to use different datums in different states or counties).
This is why we don't have one set of coordinates for the whole world...yet.
This means that our current problem is two fold –
-
That within our own country we have to use both modern and historical data which is created in different coordinate systems with different accuracies; and
-
that we work in an international world where we not only use information from different times but also different countries.
This is why it is important to respect coordinate systems and use them properly. The future looks set to have an international system which is both accurate and coordinated. Science and mathematics has made great advances towards this through the use of satellites, gravity measurements and measurments to space -VLBI, LLR and other acrnyms. (Check out the NASA video on the links page). But for the users of spatial information over the next 50 years or longer, we will continue to use a mix of maps and data with different refernce systems, so therefore have the need to consider - ‘how has the coordinate been calculated for that position?’.
So we take our mesh of grid coordinates, designed as the product of ITRF, GRS80, and GDA94 and we roll it out on paper and tweak it a bit to create a square grid over the land. The coordinates describing the grid lines are called ‘Eastings and Northings’. Each of the grids represents 6 degrees of longitude by 8 degrees of latitude with the exception of the far north/south. The grid does not cover the Polar Regions.
This is much easier for many people to understand as the positions are described in meters which are more recognisable in today's society. So what do we call this final product? We call it MGA94 – Map Grid of Australia. This is the term used when using the datum GDA as it is the main ingredient for the map. If we were using another datum such as AGD then our final product would be called AMG.
2. With the system of measurement described as the mesh of coordinates over the land mass, how do we deal with land movement? Land moves under the mesh and the coordinate of each location is no longer over the same land location. Land movement over time is monitored and after a number of years the coordinate system is updated to account for the movement. That is why we have numbers after the datum name - it is a time stamp. GDA94 is the datum which showed the coordinates of monitored locations on land at the date 1 January 1994. This is the date that the positions measured around Australia by the Australian Fiducial Network (AFN) were referenced to other positions measured around the world by the ITRF92. Over time Australia moves and no longer matches the ITRF positions. In the future it is likely that a datum will be released which anticipates the movement of Australia and updates the coordinates of positions accordingly, this is called a 'Deformation Datum'. New Zealand already uses a deformation datum and other datum tools to manage the dynamic landscape.
In the past we had other datums which were correct at previous dates. To make it more confusing, at each new release of a datum, sometimes the position of the mesh moves and the land moves but not together. The land moves due to tectonic processes but the mesh moves due to advances in technology which have helped us better pin point the centre of the earth and it’s shape.
This is why we have to keep updating the coordinates of each point on the land. The land has moved but the in some cases coordinate mesh has also moved or a different ellipsoid has been used to model the whole thing.
Why can't coordinates stay with their position on earth? - because land on earth is moving in all different directions & speeds. Check out the picture below showing the movement of New Zealand:




